The Minimum Viable Product (MVP) is a key concept in the Lean Startup framework. In many MVP sprints and workshops the question came up: How elaborated, worked-out, designed, complete must the MVP be to be released, to generate valid feedback? Do we have to user proper grafics, or a stockphotos enough? Do we need good copy, or can we use Lore Ipsum? Does it have to be a proper “brand” or URL, or can we use any?
I think it is a crucial question, because time for both a MVP and in a sprint is the (artificially) scarcest thing, and everything you can leave out helps you. At the same time, if necessary parts are missing, the MVP experiment may fail, not because the valua proposition is irrelevant, but because the design of the MVP is insufficient, thus creating wrong results (and in the worst case dropping the idea).
My standard answer has been: It needs to be good enough. It needs to convey the value proposition to the user, everything else can be in a minimal fashion. However, this was not always clear or convincing or satisfying. And all those famous MVP examples (inclusive the wonderful Zappos concierge MVP) are sometimes difficult to apply to the own project.
So when I was reading his amazing book “Shape”, Jordan Ellenberg is discussing the concept of topology, where a circle does not have to be perfect to be a circle. And when he showed and described one proof for the famous Pythagorean Theorem, I found a wonderful “illustration” of “good enough” in an MVP.
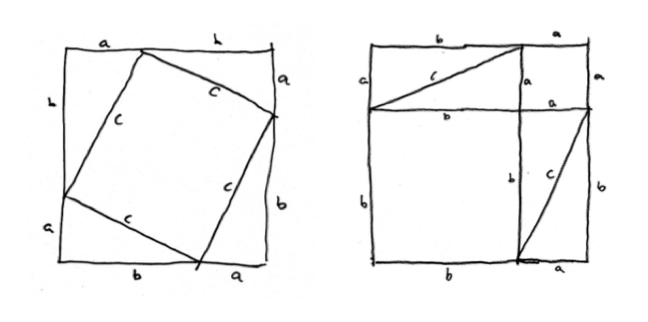
The big square is the same in both pictures. But it’s cut up in two different ways. In the first picture, you have four copies of your right triangle, and a square whose side has length c. In the second picture you also have four copies of the triangle, but they’re arranged differently; what’s left of the square is now tow smaller squares, one whose side has length a and one whose side has length b. The area that remains when you take four copies of the triangle out of the big square has to be the same in both pictures, which means that c2 (the area left over in the first picture) has to be the same as a2 + b2 ( the area left over in the second).” (p.23)
Just enjoy for a moment the “proof” of the four rectangles being the same for both boxes, the proof of the famous Pythagorean Theorem (I enjoyed it, and would have hoped to have that at old school times).
For me, a good enough MVP is exactly this: To show and to reveal the value of an idea and to surprise the user with a concept. To induce the “klick”, as we say in German (both mentally and physically).
